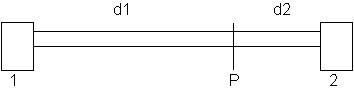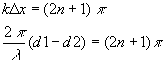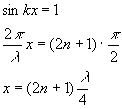Ch. 17 33 34 35 37      
Ch.18 1 5 11 13 sp1 21 41

This is updated !!! Numbers are from 5th Edition..
More Helpers
11.  First things first. Calculate the wavelength:

Next, recall the condition that the phase difference results from the path difference between the two waves in traveling from the speakers to the listener:


In the diagram above, the two rectangles represent the sources of sound, and d1 and d2 are the distances from each source to the point P where the sound from both signals is detected.
The path difference is related to the two distances shown in the following way:
.
What are the conditions for a minimum? Remember that destructive interference of the two signals occurs when the phase difference is an odd integral multiple of pi:
.
Thus,

Thus,

Here n is an integer: n = …-3, -2, -1, 0, 1, 2, 3….
Also we have another equation relating d1 and d2:

d1 + d2 = 1.25 m.

Add these two equations to solve for d1:

Solve for all the possible values of d1 by choosing the allowable values of n. Hint:
Choose positive and negative values of n so that 0 < d1 < 1.25 m.
Then, for each value of d1, calculate d2 = 1.25 m - d1.
It may be helpful to review section 18.1.
 13.

At t = 0, we get the maximum displacement. Thus,
,
since the cosine is one when t = 0.
(a) Evaluate at x = 0.25 cm
(b) Evaluate at x = 0.50 cm
(c) Evaluate at x = 1.5 cm
Antinodes occur when:

Here we assume that x is positive so that n is 0,1,2,3,…
Find the three positive, smallest values of x.
Note, you must find the wavelength. Hint:
.
sp1. The standing wave for a string is :
(0.30 m) sin(0.25x) cos(6.28t) where x is in meters and t is in seconds.. Find the wavelength and frequency of the interfering opposite traveling waves making up the total standing wave pattern.... 
sp1 hint. Compare the given expression with:

Note:
21.

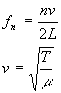Find the first 4 values of the frequency.
For practice, calculate the first four wavelengths corresponding to these frequencies.
41. See fig. 18.13. page 512, ex. 18.7. For a pipe open at one end, we have the following relationships: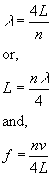


As noted in section 18.5, for a pipe open at one end, only odd harmonics are present:
n = 1,3,5,… In this problem, as in example 18.7, the wavelength is constant. Thus we achieve resonant modes by varying the length L of the air column. First, you must calculate the wavelength:

Then you must use:
,
and calculate the first two values of L that correspond to resonances. Note: These two values must be larger than 0.20 m, the minimum length of the air column.