From Spring 2000 unless indicated otherwise.

1. (20 points) A pion at rest ()decays into a muon ()and a photon (m = 0). See the diagram of the reaction below. Find the speed v of the muon after the reaction. You may use the conversion factor :


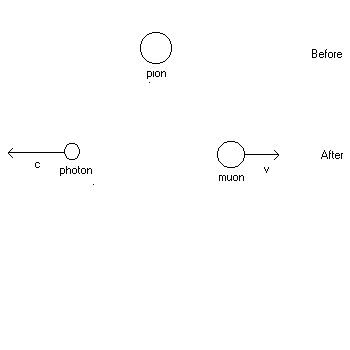
1. Solution: See hint to #43, Ch. 39, Quiz 11. Click here and scroll down the page to 43. Note that in this exam problem, the photon replaces the role of the anti-neutrino in #43 with no essential change in the formulation of the solution,  so the speed of the muon is found in the same way ! 

2. (20 points) Ch. 40 from Fall'98

This problem deals with the photoelectric effect. The stopping potential for photoelectrons emitted from a surface illuminated by light of wavelength = 491 nm
is V1 = 0.710 V. When the incident wavelength is changed to a new value , the stopping potential is found to be V2 = 1.43 V.

(a) (10 points) What is the new wavelength ?

(b) (10 points) What is the work function of the metal?

2. Solution: Note that  Kmax =eˇstopping potential = eˇVoltage.   
(a) All you do is solve two equations (A)  and (B) below for two unknowns, which are the second wavelength and the work function. The  2 equations are:

(A)

hc/    =   eV1 +  work function
(B) 

hc/     =  eV 2 +  work function
Find  the second wavelength.
(b) Find work function.

3. (20 points) Chs. 40 and 42.

A hydrogen atom in the ground state(n = 1)absorbs a photon of wavelength 97.5 nm .

Determine the maximum possible orbital angular momentum of the electron after the absorption. Note: 
. 
Thus, you need to find the lMAX allowed in the final state of the hydrogen atom after the absorption.

3. Solutions: Use the formula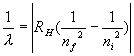

 
We are taking the absolute value.  Here nf means the index for the final state and ni  means the index for the initial state. Absolute value means that it is always positive. In this case the initial state is for n = 1  and the final state is for a larger n since the photon is absorbed and sends the atom to a higher state......Switch the order of the indices in the formula to make it positive so that ni comes first and nf comes second....
1/(97.5 x10-9)   = RH(1/12   - 1/nf2   ) ....Use RH = 1.097x107  m-1..... Solve for nf ,  which is  about 4 so set nf = 4.  Thus the  maximum value is  LMAX = 3, since L=0, 1, 2, 3, ....., n -1 for a given n.

4. (28 points) Ch. 41.

An electron in an infinite square well has a wave function given by :

,

for and zero otherwise, where L = 0.100 nm.

(a)(2 points) The wave function zero for what values of x such that 0 < x < L ? Hint: The wave function is zero when where n is a positive integer. Solve for the 2 values of x between 0 and L at which the wave function is zero.

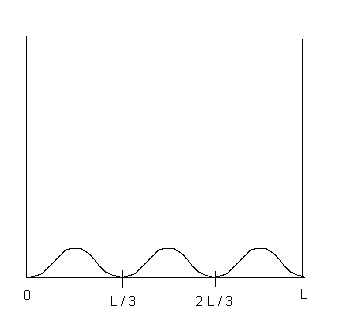
(b) (2 points) Sketch the function on the diagram provided below.

(c) (8 points) What is the probability of finding the particle between x = 0 and x = L/6.
(d) (5 points) What is the probability of finding the particle between x = 5L/6 and
x = L ? (Hint: Use symmetry)

(e) (3 points) What is the probability of finding the particle between x = 0 and
x = 2L/6 ?

(f) (8 points) What is the momentum of the particle? If you want to use the mass
for the calculation, assume the particle is an electron of mass
m = 9.11x10-31 kg.

4.  Solution:
(a)  wave function is zero for x = L/3   and x = 2L/3
(b) see sketch below
(c) integrate (wave function) 2  from 0 to x = L/6   ...use sin2u = (1 - cos2u)/2  like you did on that in-class extra credit problem.
(d) same as answer to part (c).... look at the graph below......the area under the curve is the same by symmetry...
(e) twice the answer to part (c) since twice the area under the curve in (c)..
(f) p = h/wavelength =  h/(2L/3) since L = (3/2)*wavelength ..... mass not necessary for this calculation...


5. (10 points) Ch. 43.

Consider a system of electrons confined to a three -dimensional box.

  1. Calculate the ratio of the number of allowed energy levels at 8.5 eV to the number at 7.0 eV.
  2. Copper has Fermi energy of 7.0 eV at 300 K. Calculate the ratio of the number of occupied levels at an energy of 8.5 eV to the number at the Fermi energy.
    (a) number of  allowed levels/unit volume = CE˝  ˇ dE
    ratio = CE2 ˝  ˇ dE2/CE1˝  ˇ dE1       =E2 ˝ /  E1 ˝  = 8.5˝/7.0˝  
    (b) number of occupied levels /unit volume = CE˝  ˇ dE/(e(E - EF)/kT + 1) 
    so ratio = E2 ˝  ˇ   (e(E1 - EF)/kT + 1)/  [E1 ˝  ˇ  (e(E2 - EF)/kT + 1)] where E1 =7.0 eV = EF  and E2 =8.5 eV and T = 300 K    .
6.  (20 points) Ch. 44   .from Fall'98

The nucleus undergoes alpha decay according to the reaction:

.

Take the masses to be 226.025 406 u for , 222.017 574 u for , and
4.002 603 u for

  1. (10 points) Find the Q value for this process.
  2. (5 points) Sketch the potential energy U(r) versus separation distance for the alpha particle-nucleus system.

(c) (7 points) The half-life of the radioactive nucleus is 1.6x103 years. What is the decay constant of ?

(d) (7 points) Extra Credit. If a sample of nuclei has a decay rate of 4.1x105 decays /s at t = 0, then what is the decay rate after the sample is 2000 years old? Use the fact that there are 3.13x107 s/year.

Solution:
(a) This is taken directly from an example in the book on Alpha Decay.
Q = 4.87 MeV.  Here is how you get this:
(Mx - My - Malpha )x931.494 MeV/u = 
(226.025 406 u -222.017 574 u -4.002 603 u ) x 931.494 MeV/u= 4.87 Mev
(b) See class notes and the textbook.  I sketched this on the board.
(c) 
T˝ = 0.693/.
Prove this formula!!
Find .
(d)R (at t = 0) = | dN/dt | (at t = 0) = R0  = 4.1x105 decays /s
then R = R0 et    . Evaluate at the time given.....