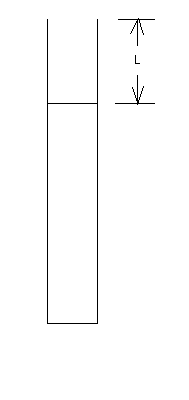
|
From Spring 2000 BELOW (CLICK HERE FOR SPECIAL SAMPLE EXAM SET PHYSICS 5 SP'12) |
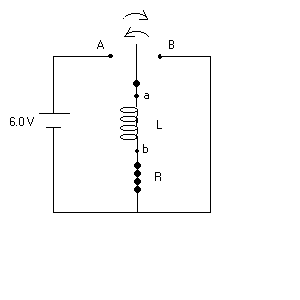
1. (30 points) A 140-mH inductor and a 4.9-ohm resistor are connected with a switch to a 6.0-V battery as shown in the figure. Initially the switch is open.
a. (7 points) If the switch is thrown to the left (connecting the battery) to position A, how much time (in seconds) elapses before the current reaches 220 mA?
b. (7 points) What is the current i in the inductor 10.0 ms seconds after the switch is closed on A?
c. (3 points) At 10.0 ms, which is larger, the voltage Va at terminal a or the voltage Vb at terminal b?
d. (5 points) Suppose the switch is kept in position to the left (position A) for a very long time (i.e. an infinite time period.) What is the value of the current at infinity?
e. (5 points) Suppose that after the infinite time period, the switch is quickly thrown from A to B. How much time elapses before the current falls to 160 mA?
f. (3 points) At the time you found in part (e), which is larger, the voltage Va at terminal a or the voltage Vb at terminal b?

| This problem is easy, based on your quizzes. For parts a and b, use the equations for a circuit with the current building up (increasing i). For part c, terminal a will be at the higher potential to oppose the increase in i. For part d, the current at infinity is simply 6.0 Volts /R, since the potential across the inductor is zero at t = infinity. Remember that the inductor potential is Ldi/dt, which is zero at infinity since the current has zero derivative at t = infinity. Parts e. and f. is for a circuit where the current is decreasing. Thus, for part f. the terminal b will be at the higher potential. |
2. (30 points) In an RLC series circuit, the resistor, inductor and capacitor are connected in series with a voltage source given by:
![]() ,
,
where 60.0 V is the maximum voltage.
The current is measured to be:
![]()
The value of the inductor is L = 220 mH and ![]() .
.
Please answer the following questions:
(a) (1 point) Is the phase angle positive or negative ?
(b) (2 points) Does the current lead or lag the voltage of the source ?
(c) (6 points) What is the average power delivered to the circuit ?
(d) (3 points) How much average heat energy (in joules) is generated during a time period of 3 minutes ?
(e) (6 points) What is the resistance R of the circuit ?
(f) (2 point) Suppose the circuit is like your car radio. You can bring the circuit into resonance by changing value of the capacitor . Would you increase or decrease the capacitor value to bring this circuit into resonance ?
(g) (7 points) What is the value of the change ![]() in the capacitance to bring the circuit into resonance?
in the capacitance to bring the circuit into resonance?
(h) (3 points) What is the value of the average power at resonance ?
| (a) positive (b) lag (c) Pav = ˝ Im*Vmcos45 = ˝ Im2 R Use R = Z cos45 and Z = 60/1.5 ohms = Vm/im . Remember rms value = max value/(square root of 2). (d) energy = power·time (e) See part (c) (f) Initially XL > Xc. We must increase Xc so that XL = Xc. Thus, decrease C since C is in the denominator of Xc. (g) This is a little tricky. First you must find C in the circuit before C changes. That's just algebra: Solve the equation tan 45 = (XL - Xc)/R . You know R from previous parts of the problem. Find initial C. Call it Co= initial C. The change in C = Cf - Co. You can get final C = Cf from the equation XL = Xc. (h) Pav = ˝ Im*Vmcos0 = ˝ Im2 R....A little tricky. Now im = Vm/R since Z = R at resonance. Remember rms value = max value/(square root of 2). |
3. (22 points) Ch. 16.
Two transverse waves are on a string described by :
y1 = 4.0 sin (3.0 x + 12 t)
and
y2 = 8.0 cos (3.0 x + 12 t)
where y1 , y2 and x are in meters and t is in seconds.
If the resultant wave can be written as,
y1 + y2 = A sin (3.0 x + 12 t + ![]() )
)
then,
a. (7 points) What is A in meters ?
b. (7 points) What is ![]() in radians ?
in radians ?
c. (2 points) What is the distance that a wave crest of the resultant wave moves in 10 seconds?
d. (2 points) Does the crest move in the negative or the positive direction?
e. (4 points) Determine the transverse velocity of the resultant wave at t = 1.0 second for the point on the string located at x = 1.0 m
| Use the same method as hints to sp1, Quiz 3. |
4. (18 points) (Ch. 17) Extra Credit
Two small speakers emit sound waves and are arranged as shown. Assume that speaker A has an output of 1.2 mW and speaker B has an output of 1.6 mW. Assume that both speakers emit sound.
(a)(9 points) How long (in seconds) does it take for the detector at point C to measure a total energy of 1.80x10 3 J ?
(b)(9 points) Determine the sound intensity level (in dB) at point C.
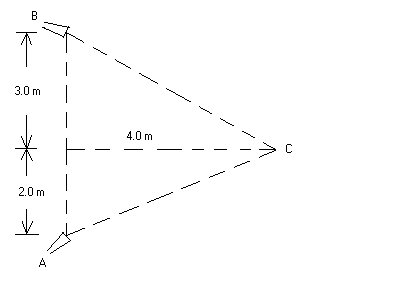
| (a) Energy = power · time. Power = (1.2+1.6) mW. This
problem is not very clear because I do not give you the effective area
of the detector. I assume that the detector can absorb all of the
energy emitted over the radii of the spherical waves from each source. A
more realistic problem would be to give you the area AD of the detector.
Then you would find the energy as (1.2 W/area of sphere A )*time*AD + (1.6 W /area of sphere B )*time*AD. I believe that I did give the area of the detector when I gave the test last Spring. You can set the detector area as AD = 1.0 cm2 Note: to get the areas of the spheres you have to use Pythagorean Theorem twice to find each radius. Nice problem! (b) Total Sound Level in dB = LevelA in dB + LevelB in dB. See equation in book on dB. Note: IA = 1.2 W/(area of sphere A) . Find LevelA in dB. IB = 1.6 W/(area of sphere B ). Find LevelB in dB. |
A tuning fork of frequency 512 Hz is placed near the top of a tube that contains water. L is the distance between the top of the tube and the water level. The tube is shown below.
Assume that the water level can be varied. Thus, L can be varied.
Assume that the water level can only be lowered. Thus, L can only be increased.
Assume that the initial value of L = 0.600 m. Thus, the minimum value of L is 0.600 m and all other values of L will be larger!
What are the first three values of L that correspond to resonant modes in the sound within the tube?