
Click here for the solutions to the real Test 3 |
1.. (20 points) Ch. 35. Hey ! Check this one out !! This problem was administered in the late 80's by me at Chabot. Light is incident horizontally and normal to the surface of the rear of a prism made of glass and follows the path shown. The ray exits the prism as shown and is incident on a mirror. The prism has the apex angle of 4-degrees shown. What is the angle of incidence of the ray on the mirror? n for glass = 1.53.

|
From Spring 2000 |
2.(30 points)
An upright image stands 1.0 m in front of a converging lens of focal length f1 = 0.50 m, which is 2.5 m from a concave mirror of focal length f2 = 0.50 m. See the diagram below. Assume that the light goes through the lens, reflects off the mirror and forms a final image without going through the lens again. (In other words, make the simple assumption that the light goes through the lens only once.)
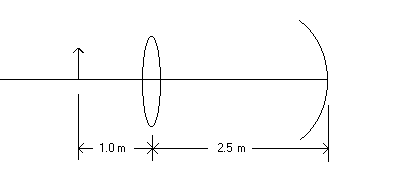
| 2. Solution: (a) 1/q1 +1/p1 = 1/f1 where the subscript 1 means the lens. f1 = 0.50 m and p1=1.0 m...find q1... then take the difference 2.5 - q1 = p2 to get p2 = object distance for the mirror, and go through the entire process again with the new p2: 1/q2 + 1/p2 = 1/f2 where f2 = 0.50 m ..........find q2. (b) Mtot = (-q1/p1)*(-q2/p2)= (neg)*(neg)= (pos).... so upright (c) Mtot = (-q1/p1)*(-q2/p2) |
3. (40 points)
A thin film of cryolite (n = 1.35) of thickness d is applied to a camera lens (n = 1.50). See the diagram below. Assume the incident light has wavelength ![]() nm and is normal to the air-cryolite interface.
nm and is normal to the air-cryolite interface.
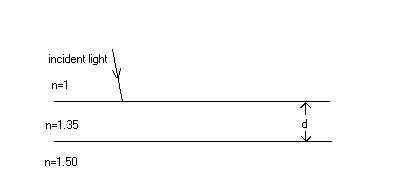
| 3. Solution: (a) 2nd = m*675 nm........ set m = 1. (b) 2nd = (m + 1/2)*675 nm.........set m = 0. |
4. (40 points) A beam of vertically polarized light with intensity I0 = 41 W/m2 is sent through 3 polarizing sheets. The vertically polarized wave is shown below moving left toward Sheet 1. The polarizing direction of Sheet 1 makes an angle of 680 with the
vertical. The polarizing direction of Sheet 2 makes an angle of 420 with the horizontal.
The polarizing direction of Sheet 3 is vertical.
What is the intensity of the transmitted light after passing through Sheet 3?
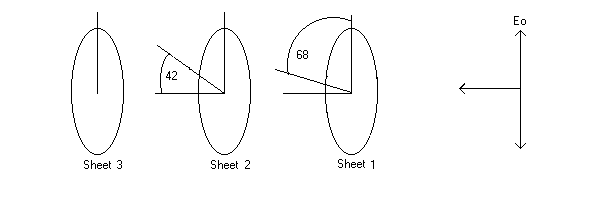
| Solution: 4. I1 = I0cos2 68 and I2 = I1cos2(68-48) and I3 = I2cos2(90-42)...be careful on that second sheet--- need 90 - 42 = 48 degrees first... |
5. Extra Credit. 15 points
A space ship whose rest length is 300 m is approaching the earth at a speed of 0.20 c with respect to the earth. Note: 300 m is the length of the ship as measured by a passenger on the ship. A meteorite, with speed 0.92c with respect to the earth, is in front of the ship moving in the opposite direction. It passes the ship on the parallel track.
How long does it take the meteorite to pass the spaceship as measured by a passenger on the ship? See the diagram below.
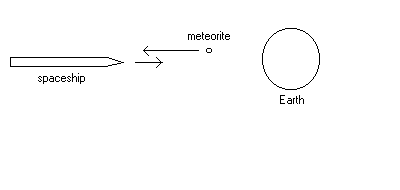
| Solution: 5. Relative speed of the meteorite with respect to the ship is: (0.20c + 0.92c)/[1 + 0.20*0.92] = 1.12c/1.184 = 0.946c so that time = (300 m)/0.946c |